“AI feels magical, until you realize it’s mostly linear algebra.”

I learnt that when people interact LLMs, it can feel like intelligence: understanding, creativity, reasoning.

But under the hood?

It’s math!

Not magic. Not consciousness. Not a digital brain.

Just math — and beautiful math at that.

1) Everything starts with vectors⌗

LLMs don’t “understand” words the way humans do. They convert text into vectors — lists of numbers.

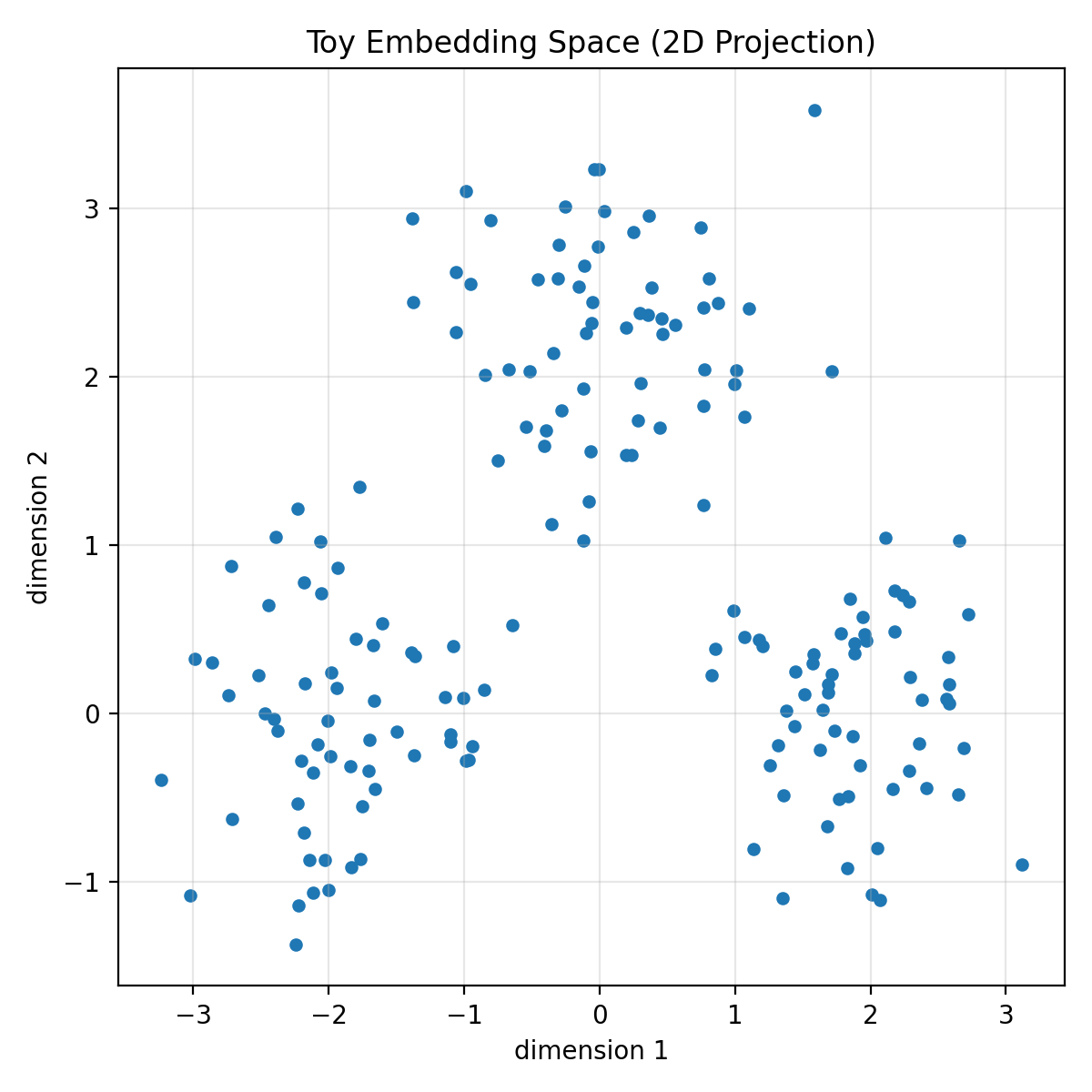
Toy embedding space (2D projection)

For example:

"king"  -> [0.21, -0.84, 1.33, ..., 0.02]
"queen" -> [0.25, -0.79, 1.40, ..., 0.04]

Each token becomes a point in a high-dimensional space (often hundreds or thousands of dimensions). The wild part is that meaning becomes geometry. Relationships show up as vector arithmetic:

$$ \text{king} - \text{man} + \text{woman} \approx \text{queen} $$

That’s linear algebra working in semantic space.⌗

2) Matrices are the real workhorses⌗

If vectors are points, matrices are transformations.

Here’s a visual intuition: a matrix transforms a grid.

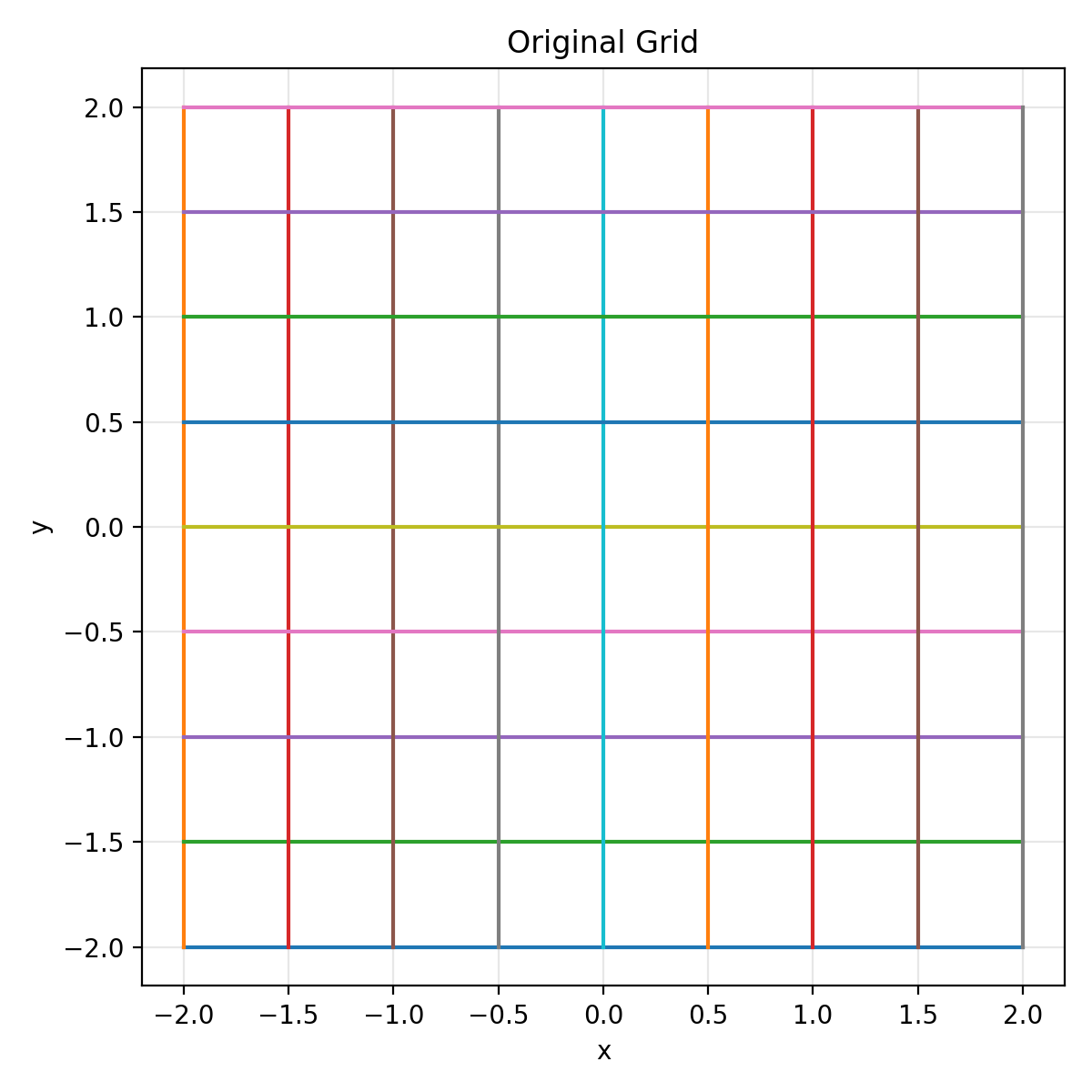
Original grid

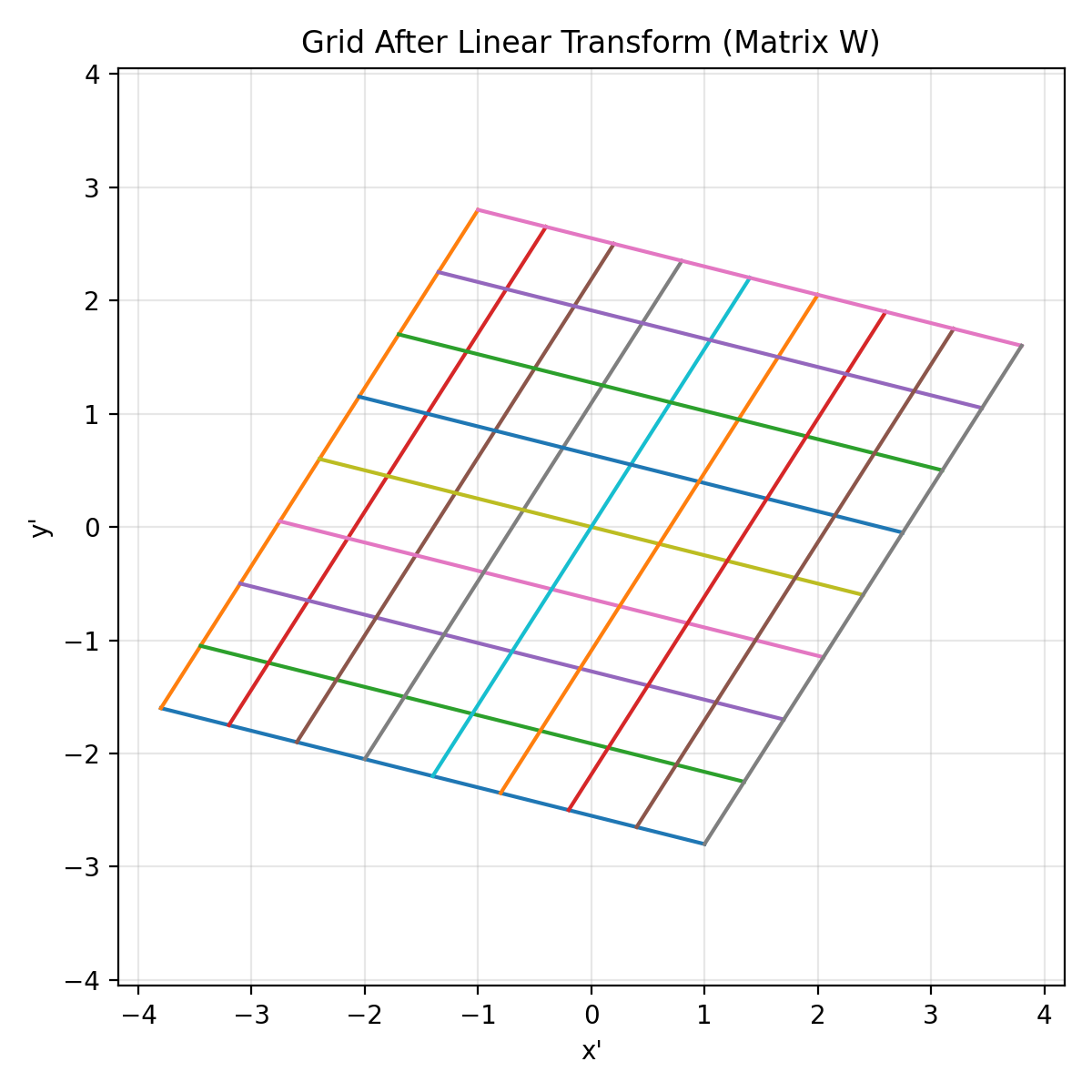
Grid after linear transform (matrix W)

A neural network layer is often described as:

$$ y = xW + b $$

Where:

  • $x$ is an input vector
  • $W$ is a weight matrix (millions or billions of learned numbers)
  • $b$ is a bias vector
  • $y$ is the transformed output

When people say:

“This model has 70 billion parameters.”

They mean:

“There are 70 billion numbers in matrices (and vectors) inside the model.”

Training is “just” learning those numbers.

3) Attention is still just math (dot-products + softmax)⌗

Modern LLMs are based on the Transformer architecture (introduced in 2017). The key idea is attention: the model computes how strongly each token should relate to every other token.

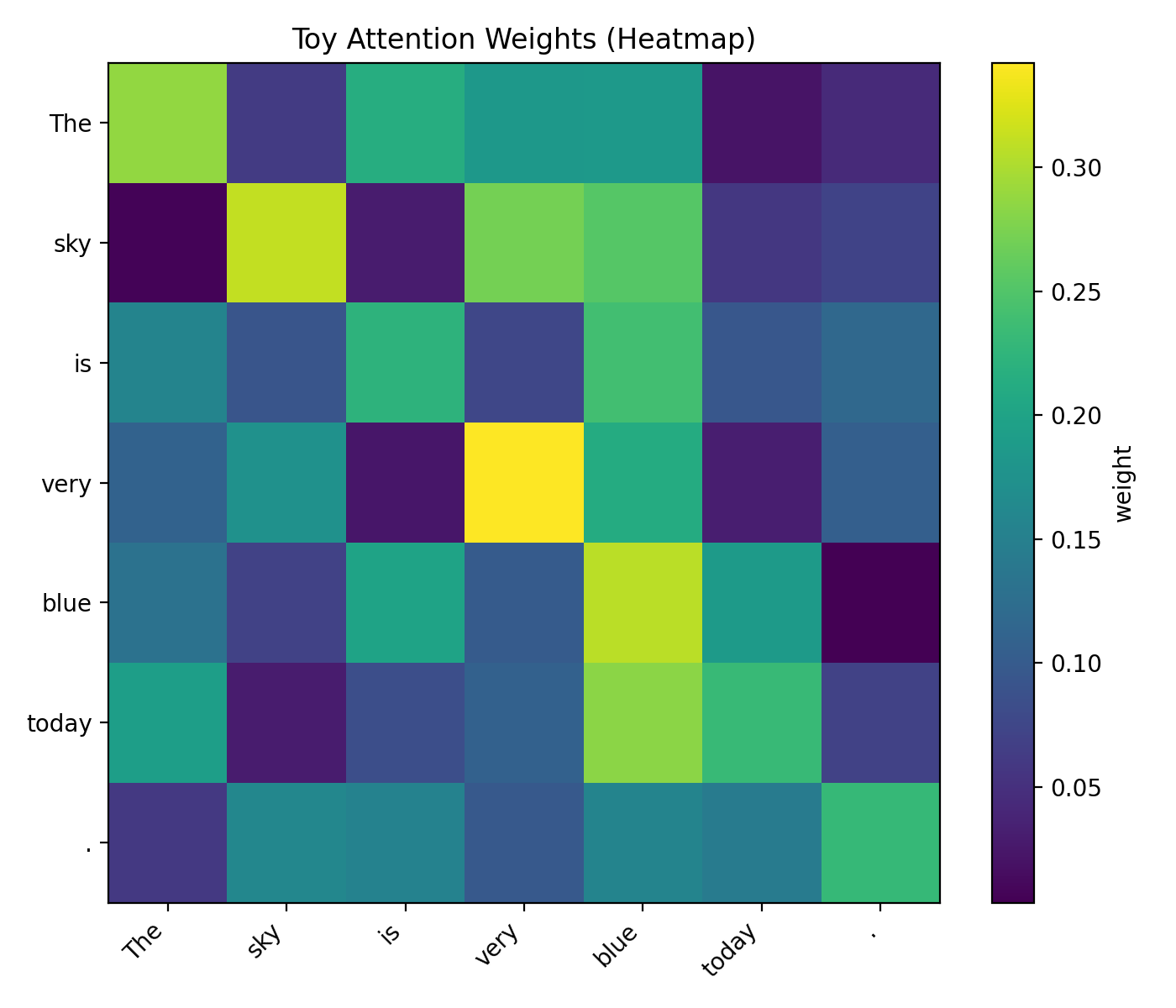
Toy attention heatmap

The core formula (scaled dot-product attention) is:

$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d}}\right)V $$

What that means in plain English:

  • compute similarities via dot-products ($QK^T$)
  • scale them ($\sqrt{d}$) so things don’t blow up
  • normalize into probabilities with softmax
  • mix the values ($V$) using those probabilities

It’s matrix multiplication, normalization, and more multiplication.

Math all the way down.

4) LLMs predict the next token (probability, not certainty)⌗

At its core, an LLM is a probability machine.

Given a prompt like:

“The sky is”

it produces a probability distribution over the next token.

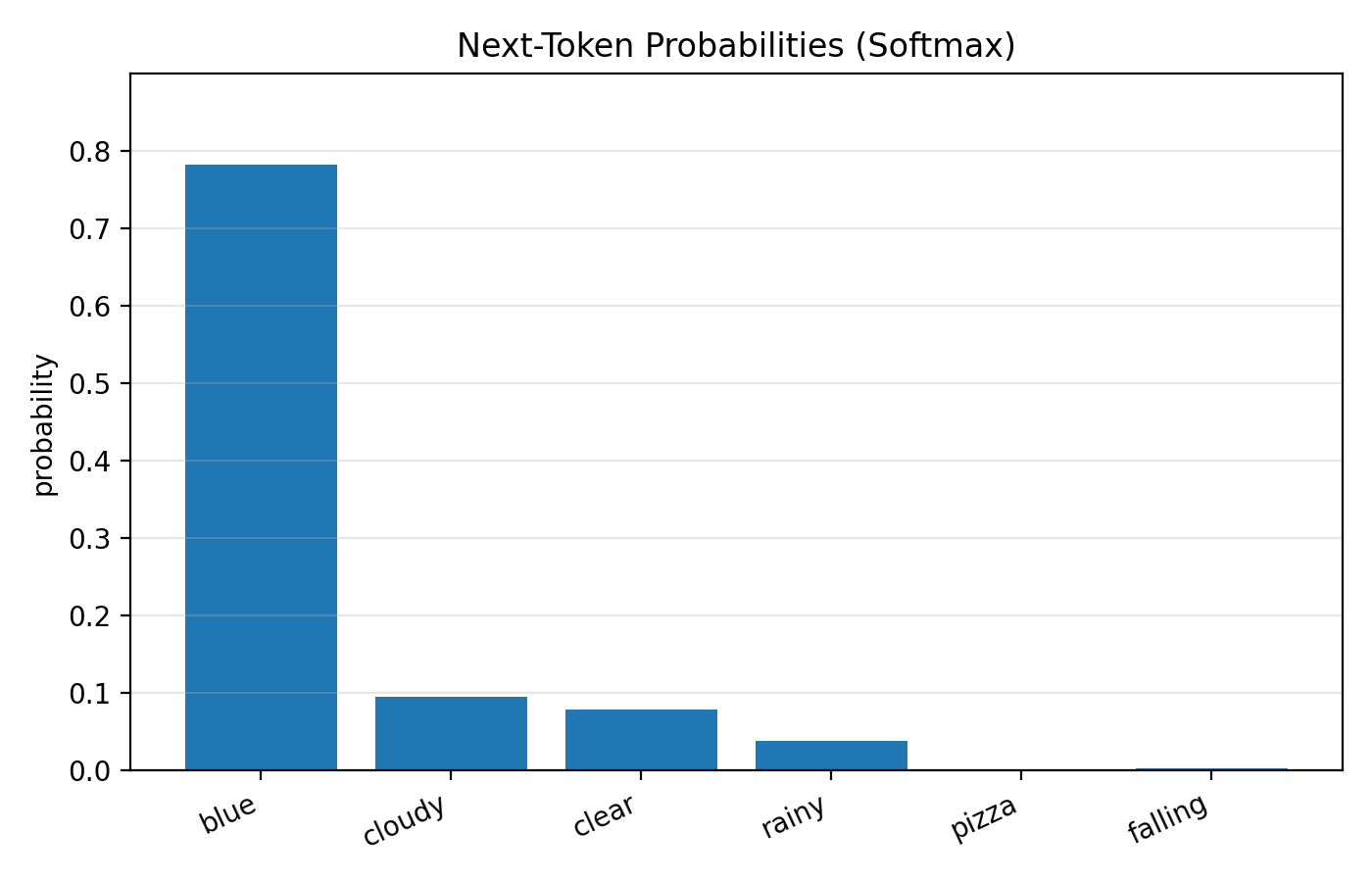
Softmax probabilities

The final layer uses softmax to convert scores (“logits”) into probabilities:

$$ p_i = \frac{e^{z_i}}{\sum_j e^{z_j}} $$

Training minimizes cross-entropy loss — a way to measure how wrong the predicted distribution is compared to the true next token:

$$ \mathcal{L} = -\sum_i y_i \log(p_i) $$

Then optimization (gradient descent) adjusts parameters to reduce that loss.

Which is… calculus and optimization.

5) So where does “intelligence” come from?⌗

There is no single place in the model that contains:

  • grammar rules
  • facts about Spain
  • knowledge about GPUs
  • a hard-coded reasoning engine

Instead, those behaviors emerge from:

  • linear algebra (vectors + matrices)
  • non-linear functions
  • probability distributions
  • gradient-based optimization
  • scale (lots of data + lots of parameters)

That’s the surprising part:

Not that it “thinks” like us — but that math at scale can produce behavior that feels like thinking.

6) Why this matters if you’re learning AI⌗

It’s easy to feel overwhelmed by buzzwords:

  • Transformers
  • RLHF
  • fine-tuning
  • agents
  • multimodal models

But the foundation is compact:

  • Linear algebra
  • Probability
  • Calculus
  • Optimization

If you understand:

  • what vectors represent
  • what matrix multiplication does
  • what a derivative tells you
  • what a probability distribution means

you understand a huge chunk of modern AI.

The rest is mostly engineering choices and scale.

7) LLMs are math⌗

There’s something empowering about this:

  • AI isn’t mystical.
  • It isn’t unreachable.
  • It isn’t reserved for a “priesthood”.

It’s math.

And math is learnable.

The next time you see a model produce a surprisingly elegant answer, remember:

Behind those words is a giant pile of matrices multiplying vectors at insane speed.

And somehow… that’s enough.